EZ-Fit software for Nonlinear Regression, Curve-fitting

Purchase EZ-Fit $49.99 - New Version  

Version 14.3    (June 1, 2025) 
All users of EZ-Fit are encouraged to download the latest version. Users with an active license can download and activate the software with their current activation code. If anyone encounters an issue with EZ-Fit, please let us know via email (DrFrank88@gmail.com).

EZ-Fit performs nonlinear regression curve-fitting of data to User-Defined Functions (UDF). Nonlinear regression is an iterative process of adjusting the model parameters such that the data best fits the UDF. The UDF can have up to eight parameters (P1...P8) and three independent variables (X1...X3). For example, y = (P1-P2) / (1 + 10^(P3*(X1 - P4))) + P2 .

EZ-Fit is priced to make it affordable to professionals and students alike. But don't let the low price mislead you. EZ-Fit is robust and powerful using some of the most sophisticated regression algorithms, including Variable Metric Quadratic Programming, Marquardt-Levenberg, Conjugate Gradient , Hooke-Reeves, Random Search, Differential Evolution and Nelder-Mead Simplex methods. Why pay hundreds and  yearly license fees when you can have curve-fitting software for a fraction of the cost. Best of all, there are no time limit restrictions or number of uses. With just a couple of clicks of the mouse, EZ-Fit simplifies curve fitting your data to UDF models. EZ-Fit does the rest by fitting the curve to your data set, displaying the statistical results, model parameters, the best fit curve, and the residuals. Plots displayed include Y vs X, X and Y Semi-logarithm, and Residuals of the best curve-fit. The EZ-Fit results of your curve-fit include the fitted  parameters, their standard errors , confidence limits, correlation matrix, and corrected Akaike value. 

EZ-Fit Nonlinear Regression Curve-fitting Software

EZ-Fit is a nonlinear regression modeling software tool used for curve-fitting data to User-defined Functions (UDF). The software offers robust nonlinear regression capabilities at an accessible price point, making it suitable for both professionals and students. It can be commonly used in engineering, chemistry, biochemistry and pharmaceutical research to model and interpret the behavior of experimental data under various conditions. Here are some key features and aspects of EZ-Fit:
 
Key Features of EZ-Fit

UDF Models
Users can define custom equations using simple algebraic relationships with up to 8 parameters (P1…P8) and 3 independent variables (X1...X3). 

UDF Examples
y = X1^P3 / (X1^P4 + 1.0)^0.5 * EXP(-1.0 * (X1/P1)^P2)
y = (P1-P2) / (1 + 10^(P3*(X1 - P4))) + P2 

Regression Algorithm
Employs sophisticated nonlinear regression techniques such as Variable Metric, Gauss-Newton with Levenberg-Marquardt modification, Conjugate Gradient, Differential Evolution, Hooke-Reeves, and Random Search methods. 

Comprehensive Statistical Analysis
Provides detailed outputs including fitted parameters, standard errors, significance levels, confidence intervals, correlation matrices, and diagnostics for multicollinearity and residuals. 

User-Friendly Interface
Designed for ease of use, the software allows users to input data and models via text files, with results graphically displayed      through various plot types such as X-Y, Hanes-Woolf, X or Y Semi-log, and Residual plots and statistics.

High Accuracy
Demonstrated an average accuracy of over 5 decimal places when tested against several challenging datasets from the National Institute of Standards and Technology (NIST). 
 
Affordability
Priced at $49.99, EZ-Fit offers a cost-effective solution without compromising on functionality. The software is available for Microsoft Windows (versions 7–11) and operates as a standalone executable, eliminating the need for complex installations. (enzymkinetics.com)
 
Applications
Scientific Research: Used in various fields such as biology, chemistry, physics, and engineering to analyze experimental data and derive meaningful conclusions.
Chemical Research: Used in laboratories to study chemical kinetics, the rate of chemical reactions and factors affecting it like temperature, pressure, catalyst and radiation.
Biochemical Research: Used in laboratories to study enzyme behavior, reaction mechanisms, and the effects of inhibitors or activators.
Pharmaceutical Development: Assists in drug development by analyzing how drugs interact with enzymes and affect their kinetics.
Education: Useful in academic settings for teaching students about data analysis and curve fitting techniques.

Benefits
Efficiency: Streamlines the process of analyzing kinetic data, saving researchers time and effort.
Accuracy: Provides reliable estimates of kinetic parameters, which are crucial for understanding mechanisms.
Versatility: Applicable to a wide range of research areas, from basic engineering, chemistry, biochemistry to applied pharmaceutical sciences.

 Conclusion
EZ-Fit stands out as a powerful, accurate, and budget-friendly tool for nonlinear regression analysis. Its combination of advanced features and user-friendly design makes it a valuable asset for anyone involved in scientific research or education.
For more information or to purchase the software, scroll down the page.

Reference 
1. Hooke and T. Jeeves, Direct search solutions of numerical and statistical problems,  Journal of the Association for Computing Machinery, vol. 8, pp. 212-229 (1961).
2. Nelder, J.A., and Mead, R, A simplex method for function minimization, Computer Journal, 7(4): 308-313 (1965).
3. Y. Bard, Nonlinear Parameter Estimation, Academic Press, New York (1974).
4. M.J.D. Powell, A fast algorithm for nonlinearly constrained optimization calculations, Lecture Notes in Mathematics, Springer-Verlag, Berlin, 630:144{157 (1978).
5. Powell, M.J.D., Variable Metric Methods for Constrained  Optimization, In: Bachem, A., Korte, B., Grötschel, M. (eds), Mathematical Programming The State of the Art, Springer, Berlin,  Heidelberg (1983).
6. D.M. Bates and D.G. Watts, Nonlinear Regression Analysis and its Applications, Wiley, New York (1988).
7. Perrella, F.W., EZ-FIT: a practical curve-fitting microcomputer program for the analysis of enzyme kinetic data on IBM-PC compatible computers, Anal. Biochem. 174 (2): 437-47 (1988).
8. Nash JC, Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation. Adam Hilger, Bristol (1979), Second Edition, Bristol: Institute of Physics Publications (1990).
9. John C. Nash and Mary Walker-Smith, Nonlinear parameter estimation: an integrated system in BASIC, Nash Information Services (1995), Originally published in 1987 by Marcel Dekker Inc. New York.
10. K. Levenberg, A method for the solution of certain problems in least squares, Quarterly of Applied Mathematics, 2, pp. 164–168 (1944).
11. D. Marquardt, An algorithm for least-squares estimation of nonlinear parameters, SIAM Journal of Applied Mathematics, 11, pp. 431–441 (1963).
12. William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery, Numerical Recipes in Fortran 77, Second Edition (1992), Numerical Recipes in Fortran 77, The Art of Scientific Computing, Second Edition, Volume 1 of Fortran Numerical Recipes, Cambridge University Press 1986, 1992, Reprinted with corrections, 1996, 1997.
13. Storn, R. and Price, K., Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces, Journal of Global Optimization, 11, pp. 341–359 (1997).

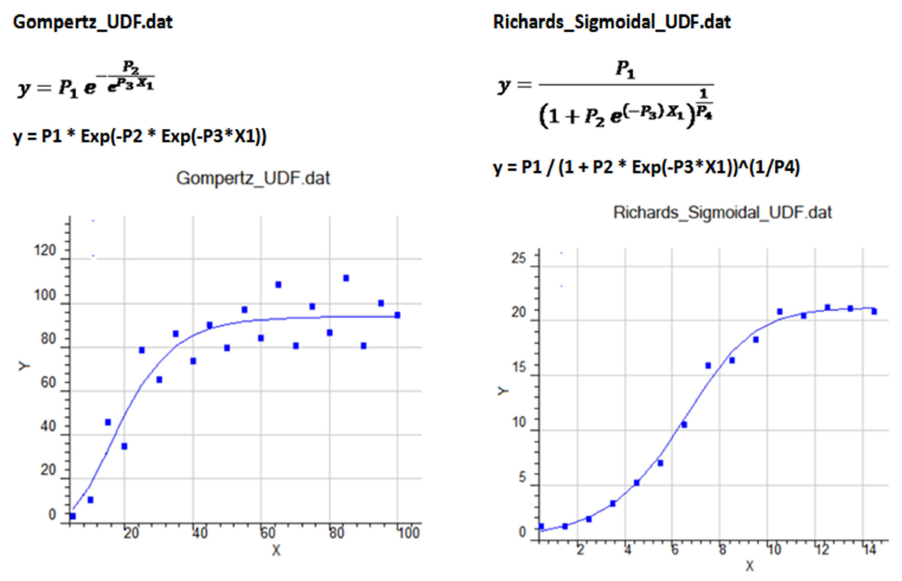
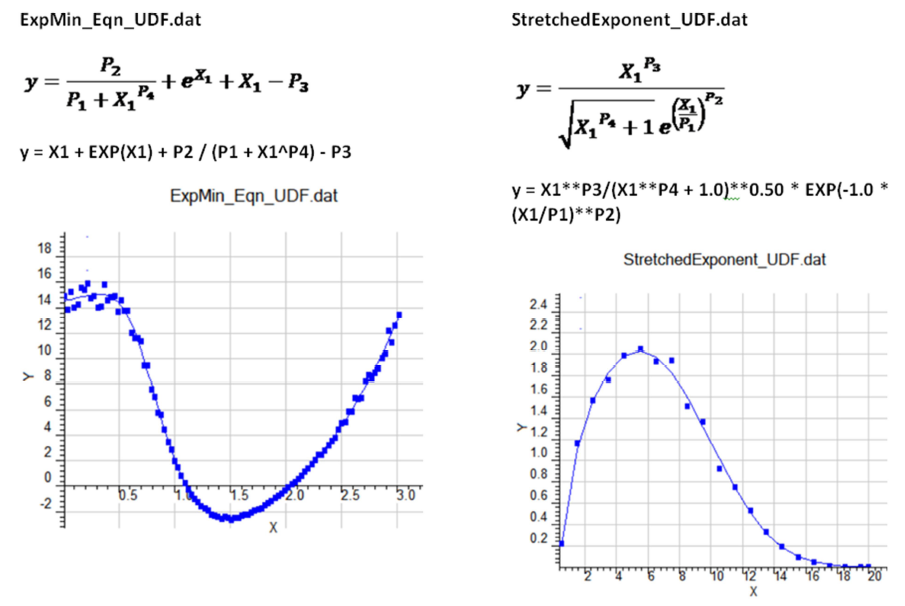
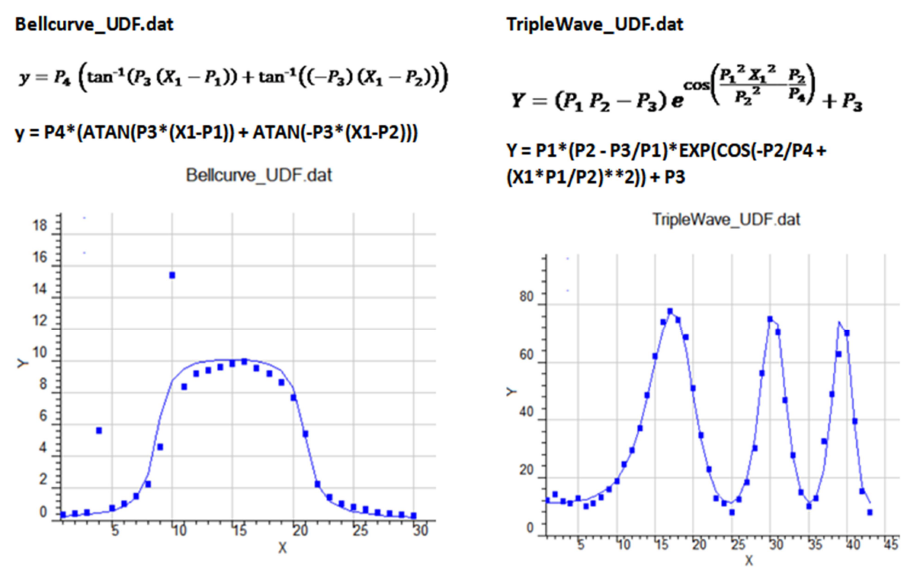
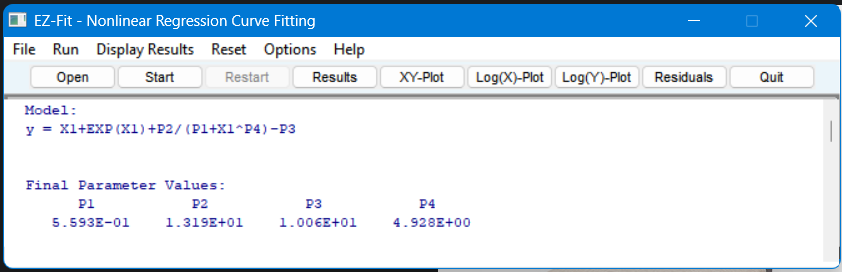
How to create a User-Defined Function Algebraically

User-Defined Function (UDF)
The UDF contains the regression model written in standard mathematical notation. Use ‘X1, X2, X3’ (case ignored) to represent the independent variable specified in the UDF. Use ‘P1,…,P8’ (case ignored) to represent the model parameters to be estimated from the data. Note that you must include a ‘Y=’ in the UDF expression. Therefore, as an example, enter y = (P1-P2) / (1 + 10^(P3*(X1 - P4))) + P2.

UDF Expression Syntax
Construct the UDF expression using standard mathematical syntax which may include the following  symbols and functions.

Symbols
+ add
- subtract
* multiply
/ divide
^ exponent ( ‘X^2’ = ‘X**2’)
() parentheses

Logical functions
(A operator B) If true, result is 1; otherwise, result is 0. The symbols a and b are replaced by the letter parameters (P1, …,P8).
< less than ‘(P1<P2)’
> greater than ‘(P1>P2)’
= equals ‘(P1=P2)’
[ less than or equal ‘(P1[P2)’
] greater than or equal ‘(P1]P2)’
# not equal ‘(P1#P2)’

Mathematical Functions
ABS(X) Absolute value of X.
ACOS(X) Arc cosine of X.
ASIN(X) Arc sine of X.
ATAN(X) Arc tangent of X.
SIN(X) Sine of X.
SINH(X) Hyperbolic sine of X.
COS(X) Cosine of X.
COSH(X) Hyperbolic cosine of X.
TAN(X) Tangent of X.
TANH(X) Hyperbolic tangent of X.
EXP(X) Exponential of X.
LOG(X) Log base e of X.
LOG10(X) Log base 10 of X.
SQRT(X) Square root of X.
OMEGW(X) Lambert Omega W of X.

Independent Variables
Use ‘X1’ in your expression to represent the independent variable. The UDF may contain up to three independent variables (X1, X2, X3). Independent variables can be only two characters long and case is ignored.

Parameters
The letter numeric combination P1 to P8 is used to represent the model parameters. Parameters can be
only two characters long and case is ignored.

Numbers
You can enter numbers in standard format such as 123.456, or you can use scientific notation
such as 1.0E-3 (which is 0.001) and 1.0E+3 (which is 1000).

Examples of valid expressions
Standard algebraic syntax is used.
y = p1*x1^p2
y = P2 / (X1^2 + P1) - P3
y = P1*X1 + P2*EXP(-P3*X2)
y = p1 - p1 * EXP(p2*x1^p3)
y = p1 / (1.0 + EXP(p2 - p3*x1))
Y = (P1-P2) / (1 + 10^(P3*(X1 - P4))) + P2
y = P1*EXP(-X1 / P3) + P2*EXP(-X1 / P4)
y = X1 + EXP(X1) + P2 / (P1 + X1^P4) - P3
y = X1^P3 / (X1^P4 + 1.0)^0.5 * EXP(-1.0 * (X1/P1)^P2)
y = P1*((X1+P3)^2 - ((X1 + P3)^4 / (P2^2)))^0.5
y = P4*(ATAN(P3*(X1 - P1)) + ATAN(-P3*(X1 - P2)))
y = P4 / (1.0 + EXP(1.0*(-P1 + P2*LOG(X1) + P3*X1))) + P5
y = (P1 + P1*P4*X1) * COS(P2*X1 + P3) * EXP(-P4*X1)
y = X1^P3 / (X1^P4 + 1.0)^0.5 * EXP(-1.0 * (X1/P1)^P2)

Data Structure
The data are typically entered in two variables: one independent variable (‘X1’) and one dependent variable (‘Y’) . Although up to three independent variables can be used (‘X1, X2, X3’). Note that the independent variable ‘X2’ is also used to identify individual data set curves.

Parameter Bounds
It may be necessary to restrict the range of parameter values that the model’s parameters can take during parameter optimization and curve-fitting. To “bound” a parameter means to give it upper and lower limits. By setting limits on parameter values during the optimization and curve-fitting, the fitting algorithm is discouraged from moving outside these limits. This reduces the chance of the regression getting stuck at a local minimum, away from the optimal solution.

Parameter Masks
Occasionally it may be necessary to mask a parameter to a fixed value. To "mask" a parameter, set the mask in the data file to "False" (meaning the parameter if fixed).  Otherwise, the parameter masks should be set to "True" (meaning the parameter is active). Masks are not case sensitive and can be displayed as "TRUE", "true", "T", or "t".

Structure of Data Files
Example #1:
Line 1: Model Function (UDF)
Line 2: Initial Parameter Estimates
Line 3: Lower Parameter Bounds
Line 4: Upper Parameter Bounds
Line 5: Parameter Masks
Line 6: X1 and Y data
Last data line must be: "END"
y = X1 + EXP(X1) + P2 / (P1 + X1**P4) - P3
1.0         1.0          1.0         1.0 
1.E-6      1.E-6      1.E-6      1.E-6 
1.e6       1.e6       1.E06     1.E6 
TRUE     true          t             T 
0.01	14.978 
0.04	13.913 
0.07	15.287 
.
.
. 
2.95	11.316 
2.98	12.693 
3.01	13.479 
END

Example #2:
y=(P1*X2-X3/P5)/(1.0+P2*X1+P3*X2+P4*X3)    !<-- UDF Model function 
40.       30.     20.     10.     0.5                         !<-- Initial parameter values 
1.E-06   1.E-06   1.E-06   1.E-06    1.E-06      !<-- Lower limits of parameters 
1.E+06  1.E+06  1.E+06  1.E+06   1.E+06      !<-- Upper limits of parameters 
TRUE    TRUE     TRUE    TRUE      FALSE       !<-- Masked parameters = TRUE or FALSE 
 25    100      20      1.83     !<-- Curve #1: X2 sets the curve #1 
 50    100      40      1.28     !<-- Data in columns: X1, X2, X3, Y 
100   100      80      0.79 
200   100      120     0.45 
400   100      180     0.25 
 25    200      20      2.38     !<-- Curve #2: X2 sets the curve #2 
 50    200      40      1.82 
100   200      80      1.25 
200   200      120     0.81 
400   200      180     0.47 
 25    400      20      2.75     !<-- Curve #3: X2 sets the curve #3 
 50    400      40      2.36 
100   400      80      1.83 
200   400      120    1.32 
400   400      180    0.82 
END                                     !<-- Enter END to identify end of file

Download the latest version of EZ-Fit

Download the software MyEZ-Fit.zip file to a single folder, unzip it and then run EZ-Fit.exe to obtain the displayed registration code that is used to unlock the software on your computer.  When you purchase EZ-Fit using PayPal, email the registration code to us at DrFrank88@gmail.com and we will send you the activation code to unlock the software on the computer where you installed it. No complicated Windows installation is required; just drop it into a folder and run. The zip file also contains example data files, and the required EZ-Fit.ini and EZ-Fit.lic files.  

Note: The generated EZ-Fit.lic file and EZ-Fit.ini files must reside in the same folder as EZ-Fit.exe.  A text editor (e.g., Notepad) must be used to create and save all input data files (MS Word should not be used). A notepad is available in the File/Edit Data File menu to open and edit name.dat files once the data file is Opened in the software. 

Download and unZip the file in a folder (e.g., C:\MyEZ-Fit\) on a computer you choose to license the software, and then run EZ-Fit.exe to retrieve the "Registration Code". The lack of formal Windows installation is intentional, as it allows installation without administrative privileges (no dynamic link libraries (DLL) are used) and no network connection is required. After you've paid for the software using PayPal, email us the Registration Code at drfrank88@gmail.com and we'll send you the Activation Code to enter and fully activate the software. Once activated, do not delete or modify the 'ini' or 'lic' files contained therein as they are required to execute and run the software. We suggest that you make backup copies of the EZ-Fit.exe, EZ-Fit.ini, and EZ-Fit.lic files for future reference.  EZ-Fit is copy-protected to run on one Microsoft Windows  32 or 64-bit computer.
Note: The EZ-Fit.zip file has been scanned by Windows Defender. 

Note: If your browser flags the downloaded zip file with a cautionary warning, you have the option of selecting "keep"  to continue the download process. The EZ-Fit.zip file was  scanned with Microsoft Windows Defender and shown not to have any detectable threats.  The EZ-Fit software does not send any information back to us or anyone else, and it does not require a network connection to run.  It is a standalone executable file (no DLL files) . 

Disclaimer of 'False Positive' virus: EZ-Fit.exe is an independently compiled and distributed program, and as such EZ-Fit.exe may not be recognized by antivirus/antimalware software and flagged as a 'false positive' by your antivirus/antimalware software. Therefore, it is advisable to create an exclusion for the EZ-Fit.exe software to avoid the appearance of 'false positive' errors during execution.

EZ-Fit Nonlinear Regression Curve-fitting Software

All users of EZ-Fit are encouraged to download the latest version. Users with an active license can download and activate the software with their current activation code. If anyone encounters an issue with EZ-Fit, please let us know via email (DrFrank88@gmail.com).

EZ-Fit Nonlinear Regression Curve-fitting Software

Reference

Nonlinear regression curve-fitting software at an affordable price.

Buy EZ-Fit below and download the EZ-Fit Software at the bottom of the page.

You may purchase EZ-Fit using PayPal or Credit Card (Visa, MasterCard, Discover, American Express).

PayPal uses the latest technology and proprietary procedures to protect the security of its transactions.

PayPal automatically encrypts your confidential information in transit from your computer to theirs.

Note: The EZ-Fit.zip file has been scanned by Windows Defender.